Understanding the Concept of an Undefined Slope
In mathematics, specifically within the study of algebra and geometry, the concept of a slope is fundamental. It describes the steepness or incline of a line and is critical for understanding linear equations and graphing. However, a particular scenario exists where the slope is considered “undefined.” This article delves into the concept of an undefined slope, explaining its significance, how it is derived, and practical examples to enhance comprehension.
What is a Slope?
Before exploring an undefined slope, it is essential to understand what a slope is in general. In mathematics, the slope of a line measures its steepness and direction. It is calculated as the ratio of the vertical change (rise) to the horizontal change (run) between two points on the line. The formula for calculating the slope mmm between two points is given by:
What is an Undefined Slope?
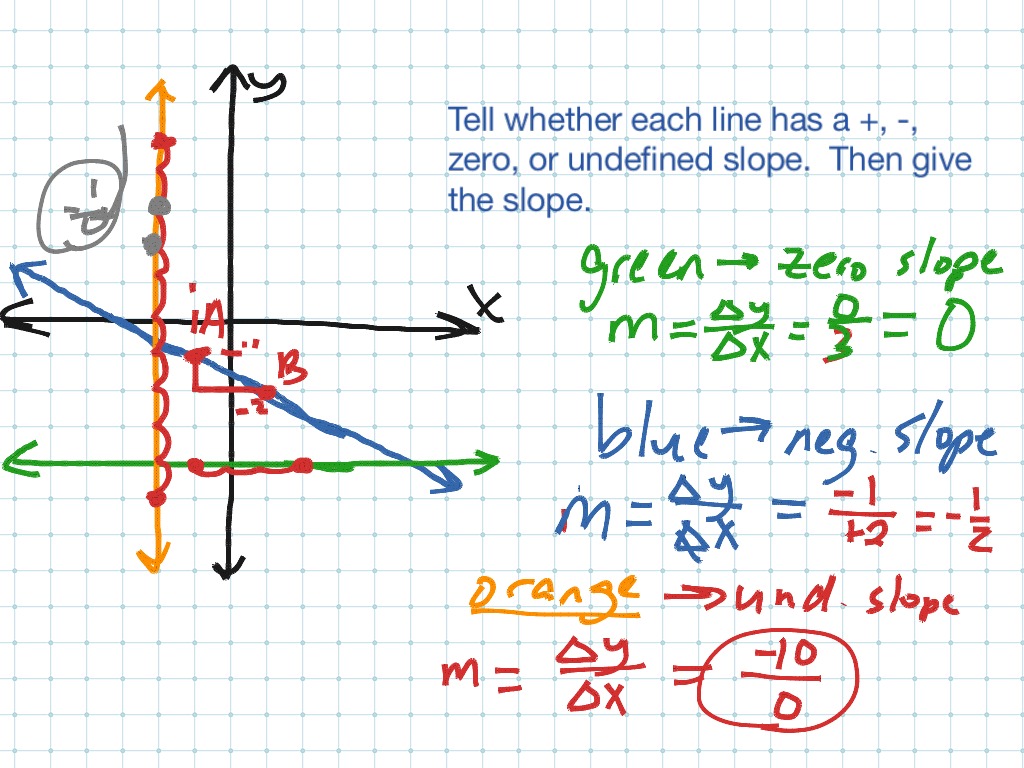
An undefined slope occurs when a line is vertical. In the slope formula, the denominator becomes zero if the difference in the x-coordinates (run) is zero. Since division by zero is undefined in mathematics, the slope of a vertical line is said to be undefined. This can be expressed as:
Characteristics of a Vertical Line
A vertical line has several distinct characteristics that set it apart from lines with defined slopes: The equation of a vertical line can be written as x=ax = ax=a, where aaa is the constant x-value for all points on the line. Vertical lines have no horizontal movement between points, meaning x1=x2x_1 = x_2x1=x2. Conceptually, vertical lines have infinite steepness because they rise indefinitely without running horizontally.
Practical Examples
Consider two points on a vertical line: (3,2)(3, 2)(3,2) and (3,5)(3, 5)(3,5). Using the slope formula: Since the denominator is zero, the slope is undefined.
Example 2: Graphing a Vertical Line
Identify the x-coordinate of 4 on the graph. Draw a straight vertical line passing through x=4x = 4x=4. Notice that no matter the y-coordinate, the x-coordinate remains 4, indicating a vertical line with an undefined slope.
Implications in Geometry and Algebra
Understanding undefined slopes is crucial in both geometry and algebra. In geometry, recognizing vertical lines helps in accurately plotting graphs and understanding the shapes and intersections of geometric figures. Algebra aids in solving linear equations and inequalities involving vertical lines.
Comparison with Other Types of Slopes
A line with a positive slope rises from left to right. For instance, a hill of m=2m = 2m=2 indicates that for every unit increase in x, y increases by two units. A line with a negative slope falls from left to right. For example, a m=−1m = -1m=−1 slope means that for every unit that increases in x, y decreases by 1 unit.
Zero Slope
A horizontal line has a zero slope, meaning there is no vertical change as x changes. The equation of a horizontal line is y=by = by=b, where B is the constant y-value.
Undefined Slope vs. Zero Slope
Vertical lines (e.g., x=5x = 5x=5) have an undefined slope due to a zero denominator in the slope formula. Horizontal lines (e.g., y=3y = 3y=3) have a zero slope as there is no change in y-values, resulting in a zero numerator in the slope formula.
Real-World Applications
In engineering and architecture, understanding the concept of slope, including undefined slopes, is critical for designing structures, roads, and landscapes. Vertical elements such as walls or support beams exemplify the practical application of vertical lines with undefined slopes.
Navigation and Cartography
Vertical lines or undefined slopes can represent features such as cliffs or straight up-and-down paths in navigation and cartography. Accurate representation and understanding of these features are essential for safe navigation and effective mapping.
Conclusion
Undefined slopes are fundamental concepts in mathematics, particularly in understanding the properties of vertical lines. Recognizing and correctly interpreting an undefined slope is crucial for various geometry, algebra, engineering, and navigation applications. Students and professionals alike can enhance their mathematical comprehension and practical problem-solving skills by grasping the characteristics and implications of undefined slopes.